用向量法解2023全国甲卷立体几何大题,不做任何辅助线-关注
 (资料图片仅供参考)
(资料图片仅供参考)
2023全国甲卷立体几何大题有非常明显的垂直关系。用几何法求解,要求作辅助线和运用立体几何公理,对创造性要求较高,对于普通学生来说不易掌握。因此在此尝试使用向量法不做任何辅助线解决此题,从已知条件出发,运用空间向量的直线推进的思维一步一步求解未知量。
题目如下:
解答过程:
以C为原点,CA、CB、CA1分别为x、y、z轴,建立空间直角坐标系设AC=x0,BC=y0,则A1C=√(4-x0^2)A(x0,0,0),B(0,y0,0),C(0,0,0),A1(0,0,√(4-x0^2))三棱柱⇒CC1=BB1=AA1=(-x0,0,√(4-x0^2))⇒C1=(0,0,0)+(-x0,0,√(4-x0^2))=(-x0,0,√(4-x0^2)),B1=(0,y0,0)+(-x0,0,√(4-x0^2))=(-x0,y0,√(4-x0^2))S△C1CB=1/2|CC1×CB|=1/2|(-x0,0,√(4-x0^2))×(0,y0,0)|=1/2|(-y0√(4-x0^2),0,-x0y0)|=y0VA1-C1CB=1/6(CB×CC1)·CA1 |0 y0 0 |=|-x0 0 √(4-x0^2)| |0 0 √(4-x0^2)|=1/6x0y0√(4-x0^2)又有V=1/3SH⇒H=3VA1-C1CB/S△C1CB=3*1/6x0y0√(4-x0^2)/y0=1⇒x0=√2(1)AC=x0=√2,A1C=√(4-x0^2)=√2⇒AC=A1C(2)A(√2,0,0),B(0,y0,0),A1(0,0,√2),B1(-√2,y0,√2),C1(-√2,0,√2)AA1与BB1的距离:|AB|·sin<AB,AA1>=|AB||AB×AA1|/(|AB||AA1|)=|AB×AA1|/|AA1|=|(-√2,y0,0)×(-√2,0,√2)|/√((-√2)^2+0^2+(√2)^2)=|(√2y0,2,√2y0)|/2=2⇒y0=√3⇒B(0,√3,0),B1(-√2,√3,√2)面BCC1B1的一条法向量:CC1×CB=(-y0√(4-x0^2),0,-x0y0)=-√6(1,0,1),取n=(1,0,1)AB1与面BCC1B1所成角的正弦值即为AB1与n所成角的余弦值:cos<AB1,n>=AB1·n/(|AB1||n|)=((-2√2,√3,√2)·(1,0,1))/(√((-2√2)^2+(√3)^2+(√2)^2)*√(1^2+0^2+1^2))=-√13/13由于二面角取锐角,故余弦值为√13/13
补充:
关于向量的叉乘见此:https://www.bilibili.com/read/cv24313606
三向量组成的平行六面体的体积等于三向量的混合积,用的也是叉乘中出现的行列式。三向量组成的三棱锥体积是平行六面体体积的1/6。
关键词:
上一篇:昆明市启动水文Ⅳ级应急响应
下一篇:最后一页
精心推荐
- 去年京津冀工信部门推进签约570多项高端高新项目
- 京津冀区域协同创新指数增长迅速
- 1至2月河北省工业生产平稳开局 规模以上工业增加值同比增长6.0%
- 浙江绍兴15日0-21时新增41例确诊病例
- 沈阳大气优良天数达近5年来最好水平
- 辽宁实行市级政府集中监管 首站定点冷库加强疫情防控
- 辽宁省25个博士后团队冲刺全国博士后创新创业大赛
- 安徽省宿州市埇桥区大营镇大营新村调整为中风险地区
- 云南哀牢山4名地质调查人员因公殉职原因查明
- 全国首部涉及“非现场执法”的法规施行 浦东新区打造引领区数字化城市治理样板
- 杭州一封控小区完成第三轮核酸检测 前两轮检测均为阴性
- 集采未中选药品现在怎么样了?这组数据告诉你
- “海归”博士后王暾:专注灾害预警科技创新 打通灾害预警“最后一公里”
- 福建宣判一起涉恶案件 10人犯罪团伙强迫交易、非法采矿获刑
-
中新网郑州12月15日电 (记者 韩章云)针对近日网友实名举报中国农业发展银行太康县支行员工夏某华吃空饷一事,中国农业发展银行河南省
-

中新网宿迁12月15日电 (记者 刘林)“房子干净又敞亮,社区漂亮又整洁。”15日,家住江苏宿迁牛角淹社区的袁有亮谈起新家,兴奋的心情
-

中新网通辽12月15日电 (记者 张林虎)15日,记者从内蒙古自治区通辽市科左后旗公安局获悉,该局打掉一个帮助网络犯罪转账的“跑分团队
-

中新网安徽阜阳12月15日电 ( 成展鹏)12月15日,规划占地面积2500亩、投资总额75亿元的安徽省阜阳市太和县保兴医药健康产业园内一片繁
-

中新网杭州12月15日电 (郭其钰 张益聪)从焦虑不安到互帮互助,浙江省杭州市上城区凯旋街道新城市广场B座里的257人经历了难忘的72小时
X 关闭
行业排行
- 1、用向量法解2023全国甲卷立体几何大题,不做任何辅助线-关注
- 2、昆明市启动水文Ⅳ级应急响应
- 3、江苏建筑职业技术学院怎么样贴吧_江苏建筑职业技术学院怎么样
- 4、天天简讯:股票行情快报:传艺科技(002866)6月21日主力资金净卖出1046.17万元
- 5、出售两家在华停产工厂,现代汽车全球战略向左中国战略向右
- 6、浙江湖州:粽叶飘香迎端午
- 7、郑州市人才主题公交地铁上线了 环球最新
- 8、“沈阳发布”入选第三届中国报业深度融合发展创新案例!_天天即时看
- 9、雪鹰领主今晚开播_最终口碑会如何呢具体是什么情况 每日播报
- 10、领益智造:终止筹划发行全球存托凭证,再融资方式变更为向不特定对象发行可转债 天天视讯
X 关闭
产业
-
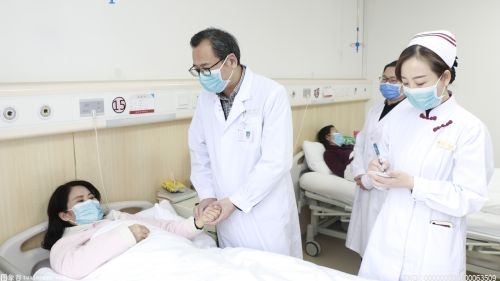
不用跑北京 在家门口也能挂上顶...
日前,我省首个神经疾病会诊中心——首都医科大学宣武医院河北医院...
-

“十四五”期间 河北省将优化快...
从省邮政管理局获悉,十四五期间,我省将优化快递空间布局,着力构...
-

张家口市宣化区:光伏发电站赋能...
3月19日拍摄的张家口市宣化区春光乡曹庄子村光伏发电站。张家口市宣...
-
“张同学”商标被多方抢注 涉及...
“张同学”商标被多方抢注,官方曾点名批评恶意抢注“丁真” ...
-

山东济南“防诈奶奶团”花式反诈...
中新网济南12月15日电 (李明芮)“老有所为 无私奉献 志愿服...
-

广州新增1例境外输入关联无症状...
广州卫健委今日通报,2021年12月15日,在对入境转运专班工作人...
-

西安报告初筛阳性病例转为确诊病例
12月15日10:20,经陕西西安市级专家组会诊,西安市报告新冠病毒...
-
广东东莞新增本土确诊病例2例 ...
(抗击新冠肺炎)广东东莞新增本土确诊病例2例 全市全员核酸检测...
-

中缅边境临沧:民警深夜出击捣毁...
中新网临沧12月15日电 (胡波 邱珺珲)记者15日从云南临沧边境...
-

“土家鼓王”彭承金:致力传承土...
中新网恩施12月15日电 题:“土家鼓王”彭承金:致力传承土家...

